What we can learn from evolving proteins
September 19, 2023
Proteins are incredible molecular machines that orchestrate almost all activity in our biological world. We are only beginning to understand them. This article is a deep dive into some statistical methods that enable us to understand new proteins by harnessing the power of evolution.
Amino acids make up proteins and specify their structure and function. Over millions of years, evolution has conducted a massive experiment over the space of all possible amino acid sequences: those that encode a functional protein survive; those that don't are extinct.
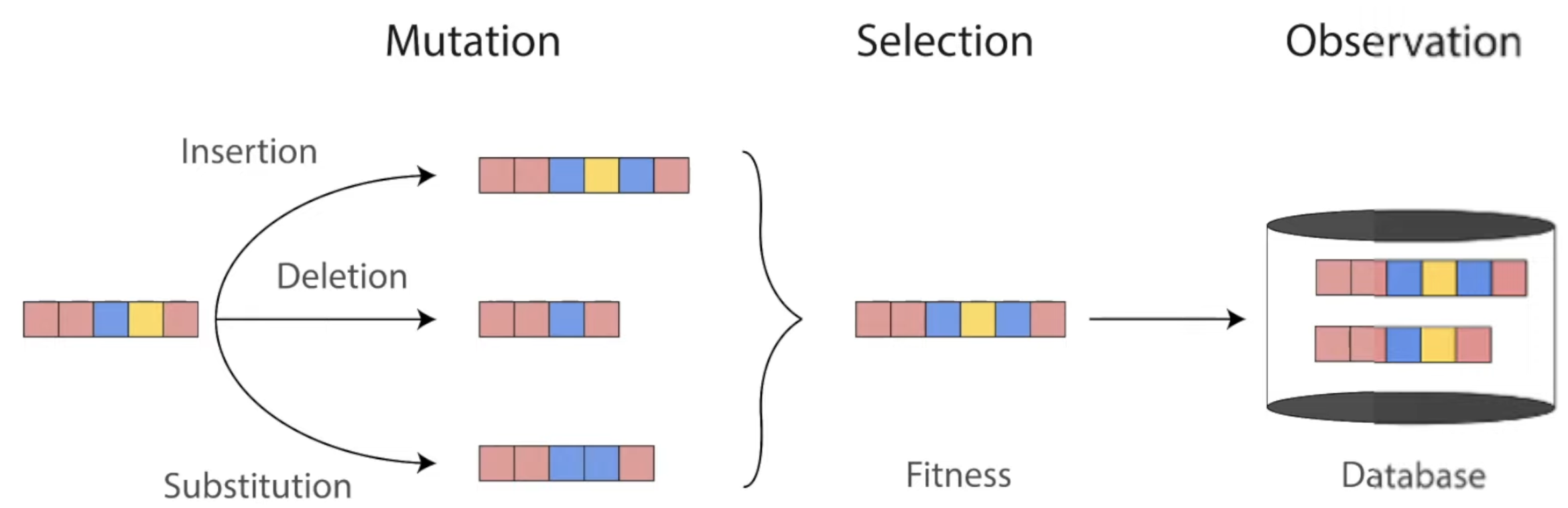
We can learn a surprising lot about a protein by studying similar variants of it we find in nature (its protein family). These hints from evolution have enabled breakthroughs like AlphaFold and many cutting-edge methods in protein design. Let's see how.
A Multiple Sequence Alignment (MSA) compiles known variants of a protein – which can come from different organisms – and is created by searching vast protein sequence databases.
MSA
One key insight is that amino acid positions that tend to co-vary in the MSA likely interact with each other in the folded structure, often via direct 3D contact. In the rest of this article, we'll dissect this MSA and make this idea concrete.
In search of a distribution
Let's start with the question: given an MSA and an amino acid sequence, what's the probability that the sequence encodes a functional protein in the family of the MSA? In other words, given a sequence , we're looking for an appropriate probability distribution based on the MSA.
Knowing is powerful. It lends us insight into sequences that we've never encountered before (more on this later!). Oftentimes, is called a model. For the outcome of rolling a die, we have great models; proteins, unfortunately not so much.
Counting amino acid frequencies
Let's take a closer look at the MSA:
Some positions have the same amino acid across almost all rows. For example, every sequence has L in the first position – it is evolutionarily conserved – which means that it's probably important!
To measure this, let's count the frequencies of observing each amino acid at each position. Let be the frequency of observing the amino acid at position .
If we compile these frequencies into a matrix, we get what is known as a position-specific scoring matrix (PSSM), commonly visualized as a sequence logo.

To evaluate some new sequence of amino acids, we can look at
should be big when the amino acid frequencies in each position of matches the frequency patterns observed the in MSA and small otherwise. For example, if starts with the amino acid L, then is contributed to the sum; if it starts with any other amino acid, is contributed.
is often called the energy function. It's not a probability distribution, but we can easily turn it into one by normalizing its values to sum to (let's worry about that later).
Pairwise frequencies
But what about the co-variation between pairs of positions? As hinted in the introduction, it has important implications for the structure (and hence function) of a protein. Let's also count the co-occurrence frequencies.
Let be the frequency of observing amino acid at position and amino acid at position .
Adding these pairwise terms to our energy function:
Now, we have a simple model that accounts for single-position amino acid frequencies and pairwise co-occurrence frequencies! In practice, the pairwise terms are often a bit more sophisticated and involve some more calculations based on the co-occurrence frequencies (we'll walk through how it's done in a popular method called EVCouplings soon), but let's take a moment to appreciate this energy function in this general form.
Actually, physicists have studied this function since the 1950s, in a different context: the interacting spins of particles in solids like magnets. The terms capture the energy cost of particles and coupling with each other in their respective states: its magnitude is big if they interact, small if they don't; the terms capture the energy cost of each particle being in its own state.
They call this the Potts model, and a fancy name for the energy function is the Hamiltonian. This fascinating field of physics applying these statistical models to explain macroscopic behaviors of matter is called statistical mechanics.
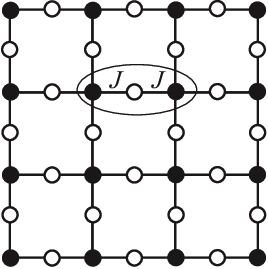
Global pairwise terms
Earlier, we considered using as the term capturing pairwise interactions. focuses on what's happening at positions and – nothing more. It's a local model. Perhaps we can imagine a scenario where positions and each independently interact with position , though they do not directly interact with each other. Because of this transitive correlation between and , the nearsighted would likely overestimate the interaction between them.
To disentangle such direct and indirect correlations, we want a global model that accounts for all pair correlations. EVCouplings is a protein structure and function prediction tool that accomplishes this using mean-field approximation 2Weigt, M et al. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U.S.A. 108, E1293–E1301 (2011).. The calculations are straightforward:
- Compute the difference between the pairwise frequencies and the independent frequencies and store them in a matrix , called the pair excess matrix
- Compute the inverse of this matrix, , the entries of which are just the negatives of the terms we seek
The theory behind these steps is involved and beyond our scope, but intuitively, we can think of the matrix inversion as an averaging step that accounts for pair correlations and makes the model global. This method is often referred to as Direct Coupling Analysis (DCA).
The distribution
We can turn our energy function into a probability distribution by 1) exponentiating, creating an exponential family distribution that is mathematically easy to work with, and 2) dividing by the appropriate normalization constant to make all probabilities sum to 1.
Predicting 3D structure
Given an amino acid sequence, what is the 3D structure that it folds into? This is the protein folding problem, a complex problem central to biology. In 2021, researchers from DeepMind presented a groundbreaking model using deep learning, AlphaFold 8Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021)., declaring the problem as solved. The implications are profound.
The EVCouplings approach to the protein folding problem cannot compete with AlphaFold in accuracy, but it is foundational to AlphaFold, which similarly relies heavily on pairwise interaction signals from MSAs.
Myriad forces choreograph the folding of a protein. Let's simplify and focus on pairs of amino acid positions that interact strongly with each other – and hypothesize that they are in spatial contact. These predicted contacts can act as a set of constraints from which we can then derive the full 3D structure.
MSA
Hovering over the blue link, we see that positions and tend to co-vary in the MSA, and they are in contact in the folded protein. Presumably, it's important to maintaining the function of the protein that when one position changes, the other also changes in a specific way – so important that failure for a sequence to do so is a death sentence that explains its absence in the MSA. Let's use the tools we have to quantify this co-variance.
Mutual information
Our is a function that takes in two amino acids: ; however, we would like a direct measure of interaction given only positions and , without a dependence on specific amino acids. In other words, we want to average over all possible pairs of amino acids that can inhabit the two positions and . To do this in a principled and effective way, we use a concept called mutual information:
where is the set of 20 possible amino acids.
Mutual information quantifies the amount of information shared by and : how much information we gain about by observing . This concept comes from a beautiful branch of mathematics called information theory, initially developed by Claude Shannon at Bell Labs in application to signal transmission in telephone systems.
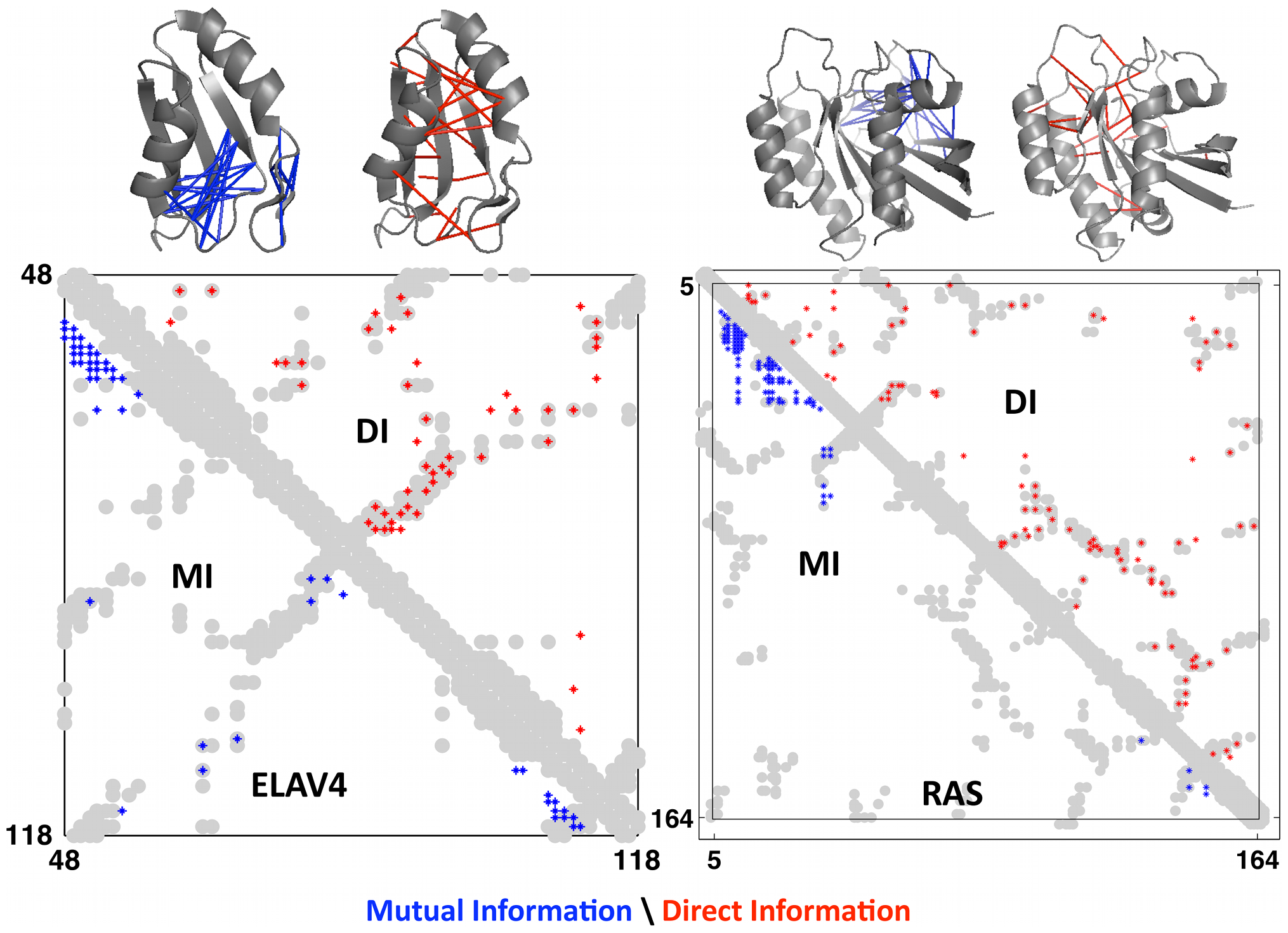
In our case, a big means that positions and are highly correlated and hence more likely to be in contact.
Direct information
As we mentioned, the local nature of can be limiting: for one, it's bad at discerning transitive correlations. EVCouplings uses a different quantity to approximate the probability that and are in contact:
where the 's are the global interaction terms obtained by mean-field approximation, and the terms can be calculated by imposing the following constraints
These constraints ensure that follows the single amino acid frequencies we observe. For each pair of positions:
-
Let's fix the amino acid at position to be L. Consider for all possible 's if we sum them all up, we get the probability of observing independently at position , which should be .
-
The same idea but summing over all 's.
Once we have , we can average over all possible 's and 's like we did for mutual information:
This measure is called direct information, a more globally-aware measure of pairwise interactions. When compared to real contacts in experimentally determined structures, DI performed much better than MI, demonstrating the usefulness of considering the global sequence context 1Marks, D.S. et al. Protein 3D structure computed from evolutionary sequence variation. PLoS One 6, e28766 (2011)..
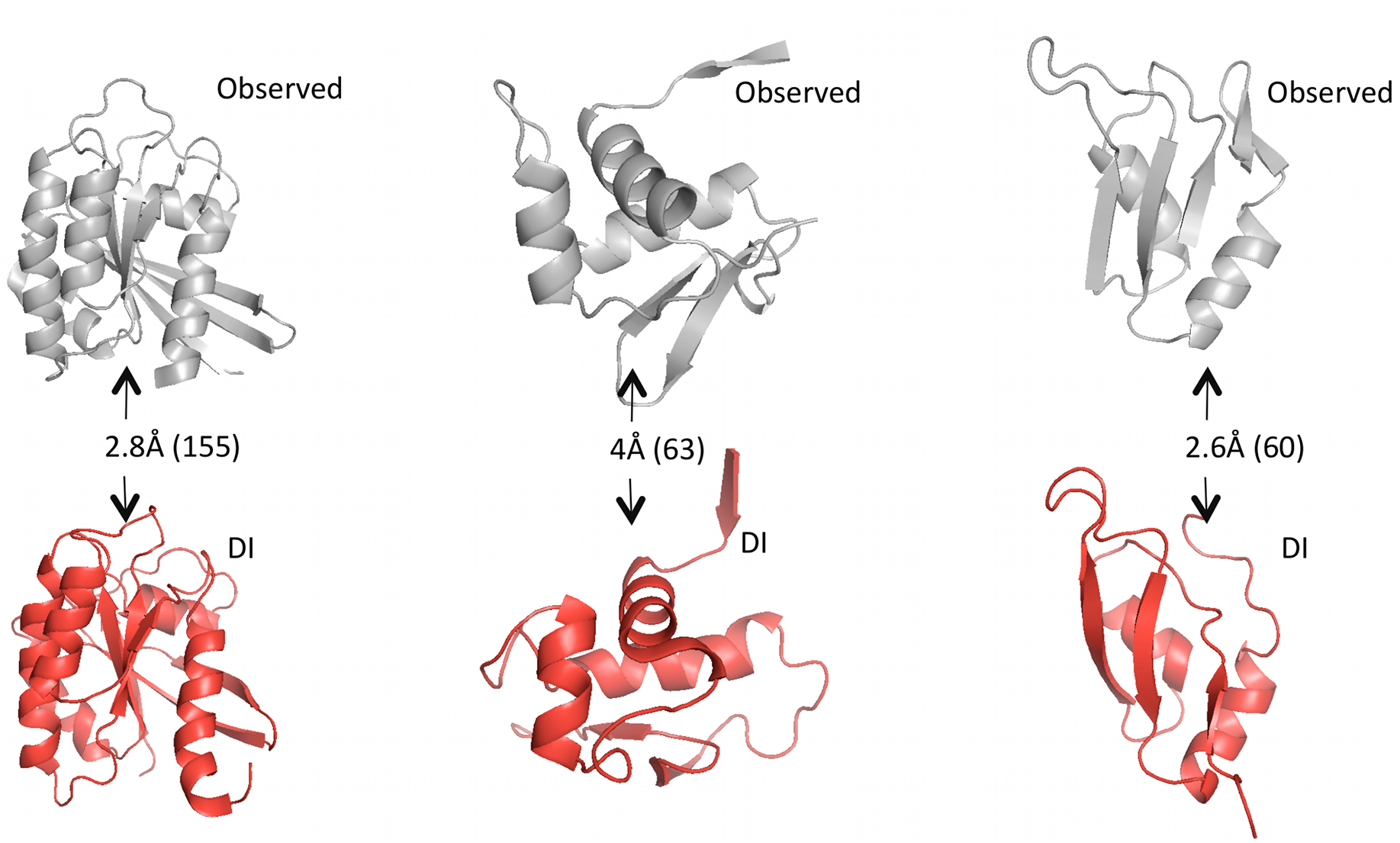
Constructing the structure
Given predicted contacts by DI, we need to carry out a few more computational steps – e.g. simulated annealing – to generate the full predicted 3D structure. Omitting those details: the results are these beautiful predicted structures that often closely match the real structures.
Predicting function
At this point, you might think: this is all neat and all, but is it directly useful in any way? One common problem in industrial biotechnology is: given a protein that carries out some useful function – e.g. an enzyme that catalyses a desired reaction – how can we improve it by increasing its stability or activity?
One approach is saturation mutagenesis: take the protein's sequence, mutate every position to every possible amino acid, and test all the mutants to see if any yields an improvement. I know that sounds crazy, but it has been made possible by impressive developments in automation-enabled high-throughput screening (in comparison, progress in our biological understanding necessary to make more informed designs has generally lagged behind). Can we do better?
Predicting mutation effects
Remember our energy function that measures the fitness of a sequence in the context of an MSA:
Intuitively, sequences with low energy should be more likely to fail. Perhaps we can let energy guide our experimental testing. Let be a wildtype, or natural, sequence, and let be a mutant sequence:
captures how much the mutant's energy improved over the wildtype.
In this paper introducing the mutation effect prediction tool in EVCouplings, researchers computed the of each mutant sequence in a saturation mutagenesis experiment on a protein called M.HaeIII 3Hopf, T. et al. Mutation effects predicted from sequence co-variation. Nat Biotechnol 35, 128–135 (2017)..
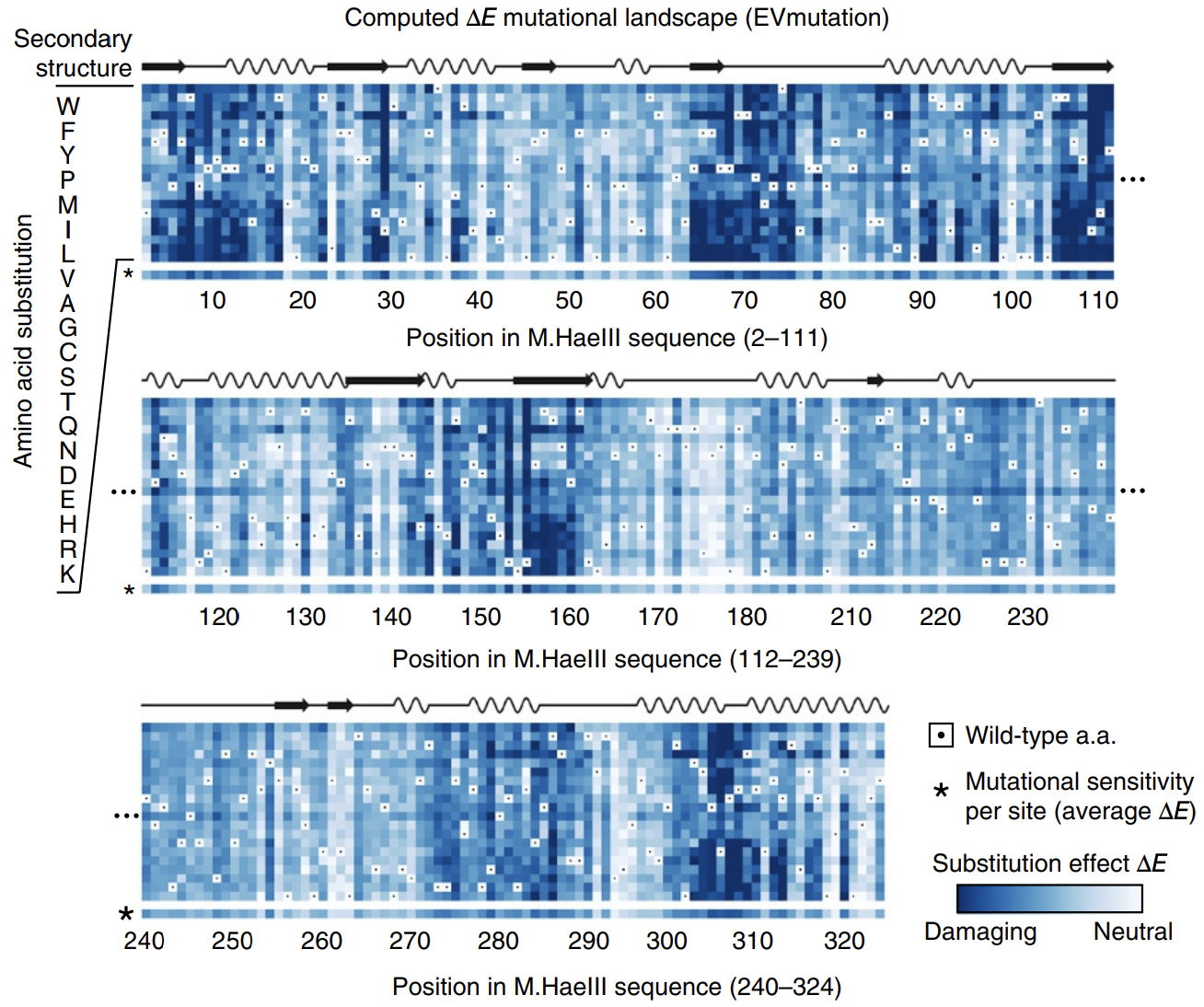
Not all positions are created equal: mutations at some positions are especially harmful. The big swathes of blue (damaging mutations) speak to the difficulty of engineering proteins.
The calculated energies correlated strongly with experimentally observed fitness (!), meaning that our energy function provides helpful guidance on how a given mutation might affect function. It's remarkable that with such a simple model and from seemly so little information (just MSAs!), we can attain such profound predictive power.
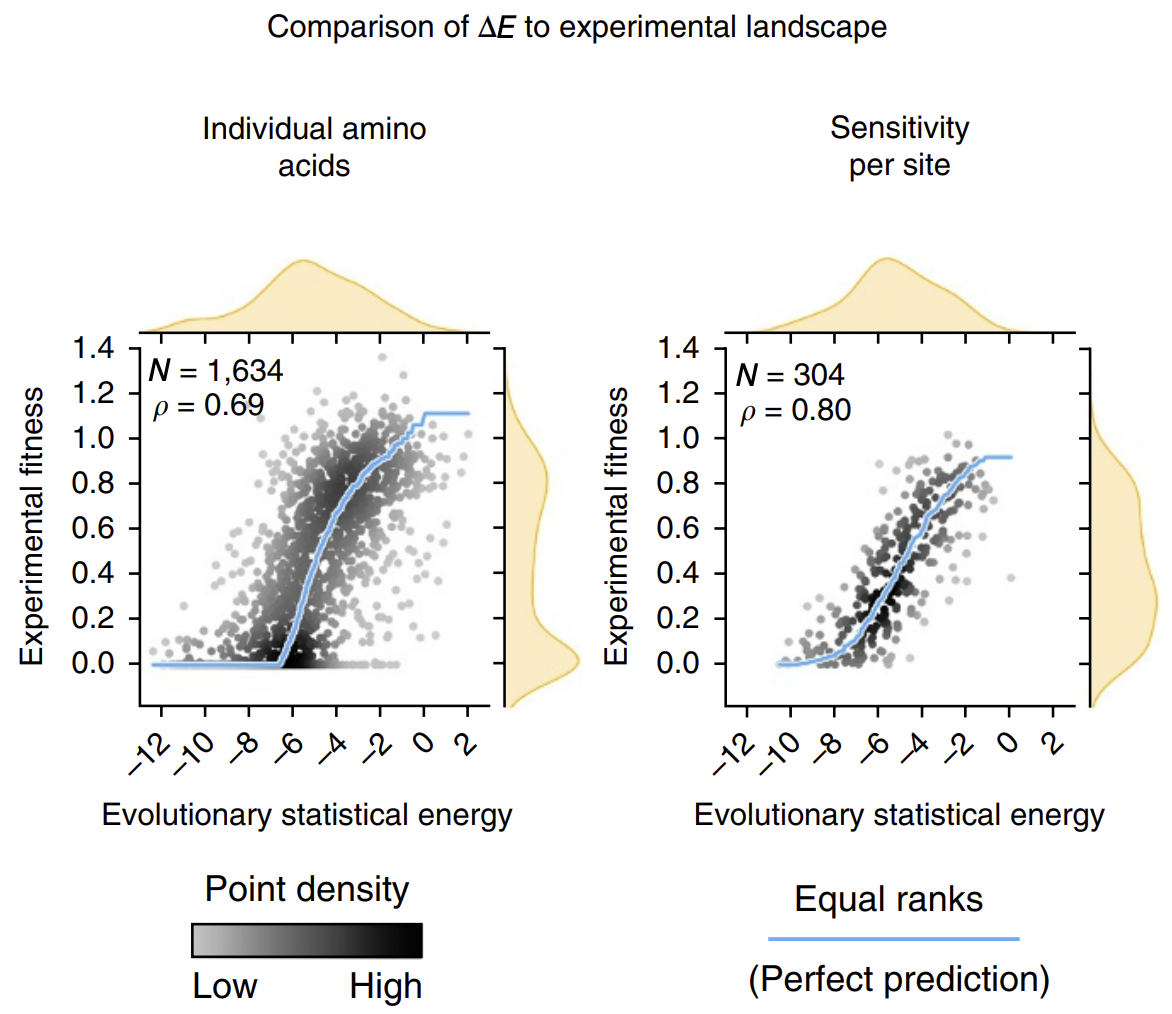
The next time we find ourselves trying a saturation mutagenesis screen to identify an improved mutant, we can calculate some 's first before stepping in the lab and can perhaps save time by focusing only on the sequences with more positive 's that are more likely to work.
Generating new sequences
Only considering point mutations can be limiting: what if the sequence we're differ at several positions from the original? To venture outside the vicinity of the original sequence, let's try this:
- Start with a random sequence .
- Mutate a random position to create a candidate sequence .
- Compare with .
- if energy increased, awesome: accept the candidate.
- if energy decreased, still accept the candidate with some probability proportional the energy difference and ideally with a knob we can control, like .
- the bigger this , which goes in the unwanted direction, the smaller the acceptance probability.
- lets us control how forgiving we want to be: makes accepting more likely; makes accepting less likely. is called the temperature.
- Go back to 2. and repeat many times.
In the end, we'll have a sequence that is a random sample from our probability distribution (slightly modified from before to include )
Why this works involves a lot of cool math that we won't have time to dive into now. This is the Metropolis–Hastings algorithm, belonging to a class of useful tools for approximating complex distributions called Markov chain Monte Carlo (MCMC).
In this paper, researchers did exactly this to with the goal of improving a protein called chorismate mutase (CM) 4Russ W.P. et al. An evolution-based model for designing chorismate mutase enzymes. Science. 2020;369(6502):440–445 (2020).. They used MCMC to draw many sequences from the DCA distribution and synthesized and tested them experimentally.
When they set (second row in the figure below), they created sequences with:
- higher energy than natural sequences (the energy they use is the negative of our , i.e. the smaller the better)
- enhanced activity compared to natural CM when expressed in E. coli (!)
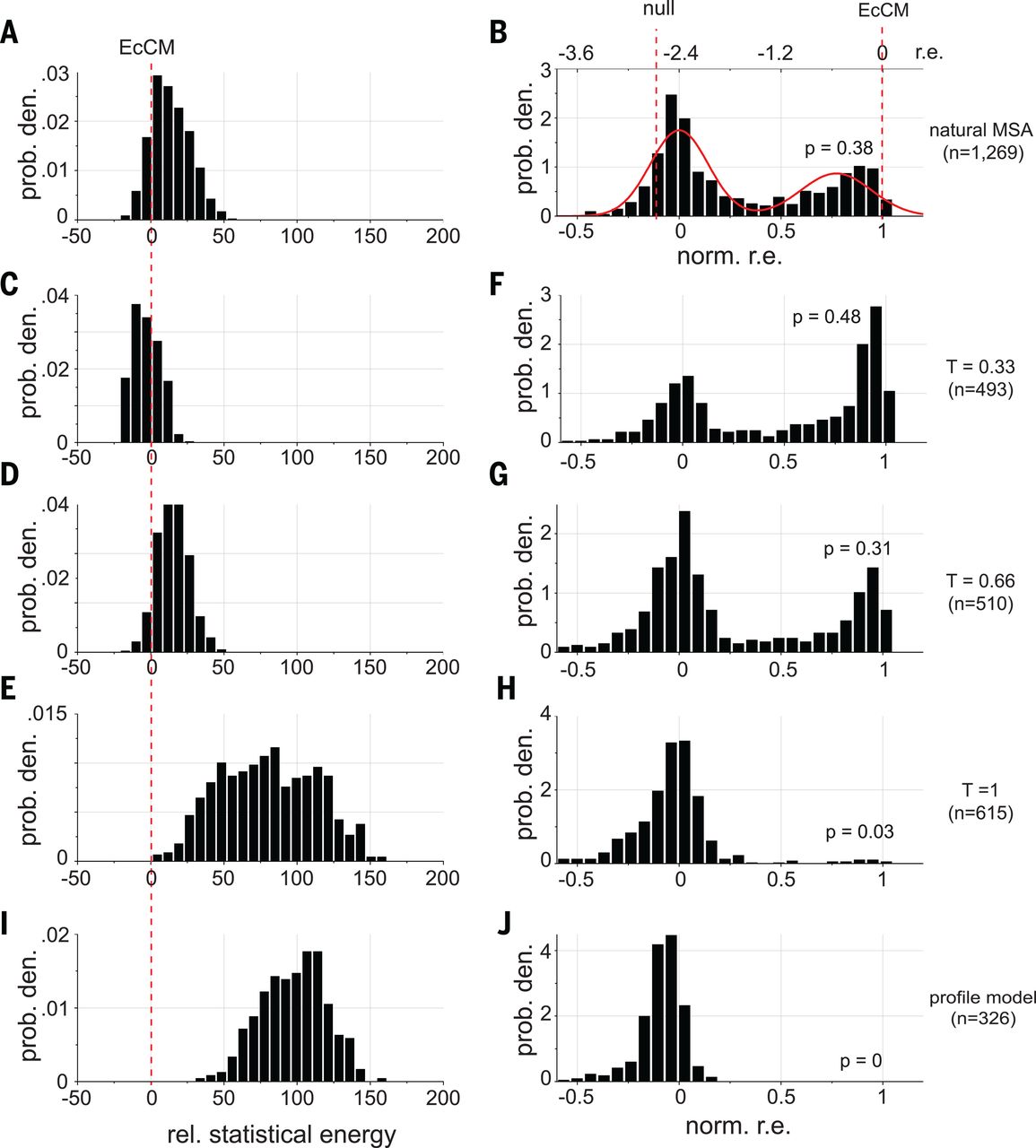
Taken together, our simple DCA model gave us the superpowers to improve on the best that nature had to offer! Our energy function enables us to not only check a given sequence for its fitness, but also generate new sequences with high fitness.
Summary + what's next
We talked about the direct coupling analysis model (DCA) with some of its cool applications. I hope by now you would join me in the fascination and appreciation of MSAs.
There are limitations: for example, DCA doesn't work well on rare sequences for which we lack the data to construct a big MSA. There are single-sequence methods like UniRep 9Alley, E.C. et al. Unified rational protein engineering with sequence-based deep representation learning. Nat Methods 16, 1315–1322 (2019). and ESM 10Rives, A. et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. PNAS 118:e2016239118 (2021). that address this problem (and come with their own tradeoffs). I will dive into them in a future post.
Recently, a deep learning mechanism called attention 5Vaswani A. et al. Attention is all you need. NeurIPS (2017)., the technology underlying magical large language models like GPT, has taken the world by storm. As it turns out, protein sequences are much like natural language sequences on which attention prevails: a variant of attention called axial attention 6Ho J. et al. Axial Attention in Multidimensional Transformers. arXiv (2019). works really well on MSAs 7Rao, R.M. et al. MSA Transformer. Proceedings of Machine Learning Research 139:8844-8856 (2021). 8Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021)., giving rise to models with even better performance. I also hope to do a deep dive on this soon!
Links
The ideas we discussed are primarily from the following papers:
-
Protein 3D structure computed from evolutionary sequence variation focuses on 3D structure prediction, describes DCA in detail, and provides helpful intuitions. It's a highly accessible and worthwhile read.
-
Mutation effects predicted from sequence co-variation presents the results on predicting mutation effects and introduces the powerful EVMutation.
-
An evolution-based model for designing chorismate mutase enzymes is an end-to-end protein engineering case study using our model.
I also recommend these papers that extend the ideas:
-
Robust and accurate prediction of residue–residue interactions across protein interfaces using evolutionary information applies this model to protein-protein interfaces, for which we need the MSAs of the two proteins side by side.
-
Evolutionary couplings detect side-chain interactions dives into some nuances and limitations of this approach: our structure prediction method using 's is mostly good at detecting interactions between side chains, and their orientations matter.
(In these papers and the literature in general, the word residue is usually used to refer to what we have called position, e.g. a protein sequence consists of a chain of amino acid residues.)
References
Marks, D.S. et al. Protein 3D structure computed from evolutionary sequence variation. PLoS One 6, e28766 (2011).
Weigt, M et al. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U.S.A. 108, E1293–E1301 (2011).
Hopf, T. et al. Mutation effects predicted from sequence co-variation. Nat Biotechnol 35, 128–135 (2017).
Russ W.P. et al. An evolution-based model for designing chorismate mutase enzymes. Science. 2020;369(6502):440–445 (2020).
Vaswani A. et al. Attention is all you need. NeurIPS (2017).
Ho J. et al. Axial Attention in Multidimensional Transformers. arXiv (2019).
Rao, R.M. et al. MSA Transformer. Proceedings of Machine Learning Research 139:8844-8856 (2021).
Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).
Alley, E.C. et al. Unified rational protein engineering with sequence-based deep representation learning. Nat Methods 16, 1315–1322 (2019).
Rives, A. et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. PNAS 118:e2016239118 (2021).